Verschiedene Möglichkeiten, den Satz des Pythagoras zu beweisen: Beispiele, Beschreibung und Übersichten

In einem kannst du dir sicher seinProzent, dass auf die Frage, was das Quadrat der Hypotenuse gleich ist, jede erwachsene Person wird kühn antworten: "Die Summe der Quadrate der Beine". Dieses Theorem hat sich in den Köpfen jedes gebildeten Menschen fest etabliert, aber es genügt, nur jemanden zu bitten, es zu beweisen, und es kann Schwierigkeiten geben. Lassen Sie uns daher verschiedene Wege in Betracht ziehen, um den Satz des Pythagoras zu beweisen.

Kurzer Überblick über die Biographie

Der Satz von Pythagoras ist fast jedem bekannt, aberAus irgendeinem Grund ist die Biographie der Person, die sie produzierte, nicht so populär. Dies ist reparierbar. Bevor man also verschiedene Wege zum Beweis des Satzes von Pythagoras studiert, muss man sich kurz mit seiner Persönlichkeit vertraut machen.

Pythagoras - Philosoph, Mathematiker, Denker ursprünglich ausAltes Griechenland. Heute ist es sehr schwierig, seine Biographie von den Legenden zu unterscheiden, die sich in Erinnerung an diesen großen Mann bildeten. Aber wie aus den Schriften seiner Anhänger hervorgeht, wurde Pythagoras von Samos auf der Insel Samos geboren. Sein Vater war ein gemeiner Steinschneider, aber seine Mutter stammte aus einer Adelsfamilie.

Der Legende nach, das Erscheinen von Pythagorassagte eine Frau namens Pythia, zu deren Ehre sie den Jungen nannten. Nach ihrer Vorhersage musste ein geborener Junge der Menschheit viele Vorteile und Gutes bringen. Was er tatsächlich tat.

Die Geburt des Theorems

In seiner Jugend zog Pythagoras von der Insel Samos nachÄgypten, um sich dort mit den berühmten ägyptischen Weisen zu treffen. Nach einem Treffen mit ihnen wurde er zum Studium zugelassen, wo er alle großen Errungenschaften der ägyptischen Philosophie, Mathematik und Medizin erlernte.

Wahrscheinlich war es in Ägypten, dass Pythagoras inspiriert wurdeMajestät und Schönheit der Pyramiden und schuf seine große Theorie. Das mag Leser schockieren, aber moderne Historiker glauben, dass Pythagoras seine Theorie nicht bewiesen hat. Er gab sein Wissen nur an seine Nachfolger weiter, die später alle notwendigen mathematischen Berechnungen vollzogen.

Was auch immer es war, heute ist nicht nur bekanntDie Technik des Beweises dieses Satzes, aber mehrere. Heute können wir nur raten, wie genau die alten Griechen ihre Berechnungen angestellt haben, also betrachten wir hier verschiedene Wege, den Satz des Pythagoras zu beweisen.

Der Satz des Pythagoras

Bevor Sie mit Berechnungen beginnen, müssen Sie herausfinden, welche Theorie zu beweisen ist. Der Satz des Pythagoras klingt folgendermaßen: "In einem Dreieck mit einem der Winkel gleich 90^o, die Summe der Quadrate der Beine ist gleich dem Quadrat der Hypotenuse. "

Insgesamt gibt es 15 verschiedene Möglichkeiten, den Satz des Pythagoras zu beweisen. Das ist eine ziemlich große Zahl, also lasst uns auf die beliebtesten von ihnen achten.

Methode eins

Lassen Sie uns zunächst angeben, was uns gegeben wurde. Diese Daten werden auf andere Methoden zum Beweis des Pythagoras-Theorems erweitert, so dass es sich lohnt, alle verfügbaren Notationen zu erinnern.

Angenommen, bei einem rechtwinkligen Dreieck mit den Schenkeln a, b und hypotenuse gleich c. Die erste Beweisführung basiert auf der Tatsache, dass ein Rechteck ein Quadrat zeichnen muss.

Um dies zu tun, benötigen Sie ein Bein der Länge azeichne ein Segment, das dem Katheten entspricht, und umgekehrt. Dies sollte zu zwei gleichen Seiten des Quadrats führen. Es bleibt nur noch zwei parallele Geraden zu zeichnen, und das Quadrat ist fertig.

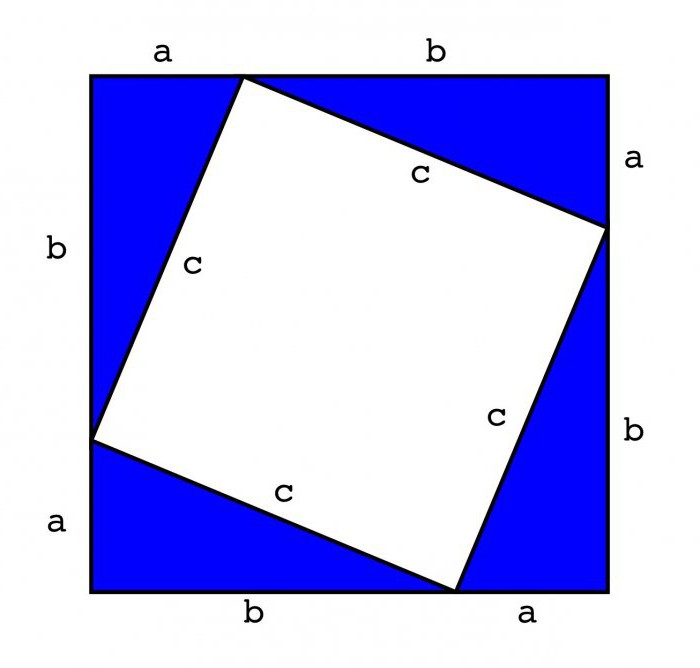
In der resultierenden Figur müssen Sie mehr zeichnenein Quadrat mit Seiten zu der Hypotenuse des ursprünglichen Dreiecks entspricht. Zu diesem Zweck wird die Eckpunkte von AC und die Kommunikation ist notwendig, um zwei gleiche Segmente mit parallelen zu ziehen. Dadurch erhielt man die drei Seiten eines Quadrats, von denen der ursprüngliche rechteckig ist die Hypotenuse Dreiecken. Docherty bleibt nur das vierte Segment.

Auf der Grundlage der resultierenden Figur können wir schließen, dass die Fläche des äußeren Quadrats (a + b) ist.². Wenn Sie in die Figur schauen, sehen Sie, dass zusätzlich zu dem inneren Quadrat vier rechteckige Dreiecke darin sind. Die Fläche von jedem ist 0.5aV.

Daher ist das Gebiet: 4 * 0.5aв + с²= 2ав + с²

Daher (a + b)²= 2ав + с²

Und folglich mit²= a²+ in²

Der Satz ist bewiesen.

Methode zwei: ähnliche Dreiecke

Diese Formel für den Beweis des Satzes von Pythagoraswurde auf der Grundlage der Aussage aus dem Geometrieabschnitt über ähnliche Dreiecke abgeleitet. Es besagt, dass der Kathete eines rechtwinkligen Dreiecks ein Durchschnitt proportional zu seiner Hypotenuse und ein Segment der Hypotenuse ist, die von dem Eckpunkt 90 ausgeht^o.

Die Anfangsdaten bleiben gleich, so dass wir sofort mit dem Beweis beginnen. Wir zeichnen senkrecht zur Seite AB ein Segment der SD. Basierend auf der obigen Aussage sind die Dreiecksbeine:

AC = √AB * AD, CB = √AB * DV.

Um die Frage zu beantworten, wie man den Satz des Pythagoras beweisen kann, muss der Beweis konstruiert werden, indem beide Ungleichungen quadriert werden.

Wechselstrom²= AB * AD und CB²= AB * DV

Jetzt müssen wir die resultierenden Ungleichungen addieren.

Wechselstrom²+ CB²= AB * (Ä * * Ä), wobei Ää + ÄD = Ä

Es stellt sich heraus, dass:

Wechselstrom²+ CB²= AB * AB

Und folglich:

Wechselstrom²+ CB²= AB²

Der Beweis des Satzes des Pythagoras und die verschiedenen Methoden zu seiner Lösung erfordern einen vielseitigen Ansatz für dieses Problem. Diese Option ist jedoch eine der einfachsten.

Eine andere Methode der Berechnung

Die Beschreibung verschiedener Arten, den Satz zu beweisenPythagoras kann nichts sagen, solange Sie selbst nicht anfangen zu üben. Viele Methoden liefern nicht nur mathematische Berechnungen, sondern auch die Konstruktion neuer Figuren aus dem ursprünglichen Dreieck.

In diesem Fall ist es notwendig, ein weiteres rechteckiges Dreieck des VSD aus dem BC zu vervollständigen. So, jetzt gibt es zwei Dreiecke mit einem gemeinsamen Bein BC.

Wissend, dass die Bereiche ähnlicher Figuren ein Verhältnis wie die Quadrate ihrer ähnlichen linearen Dimensionen haben, dann:

S_AVS * mit dem²- S_avd* in² = S_avd* a²- S_up* a²

S_AVS* (s²in²) = a²* (S_avd-S_up)

mit dem²in²= a²

mit dem²= a²+ in²

Da diese Variante aus den verschiedenen Beweismethoden des Pythagoras-Theorems für die 8. Klasse kaum geeignet ist, kann man das folgende Verfahren anwenden.

Der einfachste Weg, um den Satz von Pythagoras zu beweisen. Bewertungen

Wie Historiker glauben, war diese Methode das erste Malverwendet, um das Theorem auch im antiken Griechenland zu beweisen. Es ist das einfachste, da es absolut keine Berechnungen erfordert. Wenn die Zeichnung korrekt gezeichnet ist, dann der Beweis für die Behauptung, dass a²+ in²= s² , wird klar gesehen werden.

Die Bedingungen für diese Methode unterscheiden sich geringfügig von der vorherigen. Um das Theorem zu beweisen, nehmen wir an, dass ein rechtwinkliges Dreieck ABC ein gleichschenkliges Dreieck ist.

Wir nehmen die Hypotenuse AS für die Seite des Quadrats undTöchter drei seiner Seiten. Zusätzlich ist es notwendig, zwei diagonale Linien in das resultierende Quadrat zu zeichnen. Also, um vier gleichschenklige Dreiecke darin zu bekommen.

Zu den Beinen AB und CB musst du auch ein Kind im Quadrat haben und in jedes eine diagonale Linie zeichnen. Die erste Linie wird von der Ecke A gezeichnet, die zweite Linie wird von C gezeichnet.

Jetzt müssen Sie die resultierende Zeichnung genau betrachten. Da es an der Hypotenuse der AS vier Dreiecke gibt, die gleich dem ursprünglichen Dreieck sind, und an den Beinen durch zwei, zeigt dies die Wahrheit des Satzes an.

Übrigens, dank dieser Methode, den Satz des Pythagoras zu beweisen, erschien der berühmte Satz: "Pythagoreische Hosen sind in allen Richtungen gleich".

Beweis von G. Garfield

James Garfield ist der zwanzigste Präsident der Vereinigten Staaten von Amerika. Darüber hinaus hinterließ er als Herrscher der Vereinigten Staaten seine Spuren in der Geschichte, er war auch ein begnadeter Autodidakt.

Am Anfang seiner Karriere war er gewöhnlichein Lehrer in einer öffentlichen Schule, wurde aber bald Direktor einer der höheren Bildungseinrichtungen. Der Wunsch nach Selbstentwicklung erlaubte ihm, eine neue Theorie des Beweises des Satzes des Pythagoras vorzuschlagen. Der Satz und ein Beispiel seiner Lösung sind wie folgt.

Zuerst müssen Sie auf ein Blatt Papier zwei zeichnenrechteckige Dreieck so, dass die Katet von einer von ihnen eine Fortsetzung der zweiten ist. Die Eckpunkte dieser Dreiecke müssen verbunden werden, damit das Trapez schließlich ausfällt.

Wie bekannt, ist die Fläche des Trapezes gleich dem Produkt der Halbsumme seiner Basen zur Höhe.

S = a + b / 2 * (a + b)

Wenn wir das resultierende Trapez als eine aus drei Dreiecken bestehende Figur betrachten, dann kann seine Fläche wie folgt gefunden werden:

S = av / 2 * 2 + s²/ 2

Jetzt ist es notwendig, die beiden Anfangsausdrücke auszugleichen

2ав / 2 + с / 2 = (а + в)²/ 2

mit dem²= a²+ in²

Ein Satz von Pythagoras und die Methoden seines Beweises können nicht nur in einem Band des Lehrbuchs geschrieben werden. Aber ist es sinnvoll, wenn dieses Wissen nicht in der Praxis angewendet werden kann?

Praktische Anwendung des Satzes des Pythagoras

Leider in modernen LehrplänenEs ist beabsichtigt, diesen Satz nur in geometrischen Problemen zu verwenden. Die Absolventen verlassen bald die Schulmauern, ohne zu wissen, wie sie ihr Wissen und Können in der Praxis anwenden können.

In der Tat, um den Satz des Pythagoras zu verwendenJeder kann seinen Alltag machen. Und nicht nur in beruflicher Tätigkeit, sondern auch im normalen Haushalt. Betrachten wir ein paar Fälle, in denen der Satz des Pythagoras und wie es beweisen kann äußerst notwendig.

Die Verbindung zwischen Theorem und Astronomie

Es scheint, als könnten die Sterne und Dreiecke auf Papier verbunden werden. In der Tat ist die Astronomie ein wissenschaftliches Gebiet, in dem der Satz des Pythagoras weit verbreitet ist.

Betrachten Sie beispielsweise die Bewegung eines Lichtstrahls im Raum. Es ist bekannt, dass sich Licht in beiden Richtungen mit der gleichen Geschwindigkeit bewegt. Die Trajektorie AB, die einen Lichtstrahl bewegt, wird genannt l. Und die Hälfte der Zeit, die Licht von Punkt A nach Punkt B braucht, nennen wir es t. Und die Geschwindigkeit des Strahls - c. Es stellt sich heraus, dass: c * t = l

Wenn wir diesen Strahl von einem anderen betrachtenB. von einem Raumliner, der sich mit einer Geschwindigkeit v bewegt, dann ändert sich mit dieser Beobachtung von Körpern ihre Geschwindigkeit. In diesem Fall bewegen sich sogar feste Elemente mit einer Geschwindigkeit v in die entgegengesetzte Richtung.

Nehmen wir an, ein Comic-Liner schwimmt nach rechts. Dann bewegen sich die Punkte A und B, zwischen denen der Strahl rast, nach links. Außerdem, wenn der Strahl bewegt sich von Punkt A nach Punkt B, Punkt A Zeit zu bewegen, und dementsprechend das Licht in einen neuen Punkt C gekommen ist, die Hälfte der Strecke zu finden, an dem der Punkt A bewegt hat, ist es notwendig, die Geschwindigkeit des Schiffes in einem halben Strahllaufzeit zu multiplizieren (t ").

d = t "* v

Und um herauszufinden, wie weit ein Lichtstrahl durch diese Zeit hindurchgehen konnte, ist es notwendig, den halben Weg der neuen Buche zu bezeichnen und den folgenden Ausdruck zu erhalten:

s = c * t "

Wenn wir uns vorstellen, dass die Lichtpunkte C und B und auchder Raumliner ist der Scheitelpunkt eines gleichschenkligen Dreiecks, dann wird das Segment von Punkt A zum Liner es in zwei rechtwinklige Dreiecke teilen. Daher kann man dank des Satzes des Pythagoras die Entfernung finden, die ein Lichtstrahl durchgehen kann.

s² = l² + d²

Dieses Beispiel ist natürlich nicht das erfolgreichste, da nur Einheiten das Glück haben können, es in der Praxis zu versuchen. Betrachte deshalb banalere Versionen der Anwendung dieses Theorems.

Radius der mobilen Signalübertragung

Das moderne Leben ist ohne die Existenz von Smartphones nicht vorstellbar. Aber wie viel wäre es für sie zu proc, wenn sie nicht Abonnenten durch mobile Kommunikation verbinden könnten?

Die Qualität der mobilen Kommunikation hängt direkt davon abDie Höhe der Antenne des Mobilfunkbetreibers. Um die Entfernung vom mobilen Turm zu berechnen, kann das Telefon ein Signal empfangen, das Sie nach dem Pythagoras-Theorem anwenden können.

Angenommen, wir müssen die ungefähre Höhe eines stationären Turms finden, damit er das Signal in einem Radius von 200 Kilometern ausbreiten kann.

AB (Turmhöhe) = x;

BC (Signalübertragungsradius) = 200 km;

OS (Radius des Globus) = 6380 km;

Von hier aus

OB = OA + ABOV = r + x

Nach dem Satz von Pythagoras werden wir herausfinden, dass die minimale Höhe des Turms 2,3 Kilometer betragen sollte.

Der Satz des Pythagoras im Alltag

So seltsam es auch scheinen mag, könnte sich der Satz des Pythagoras herausstellennützlich, auch im Haushalt, wie zum Beispiel die Höhe des Schrankes zu bestimmen. Auf den ersten Blick ist es nicht nötig, solche komplexen Berechnungen zu verwenden, da Sie einfach Messungen mit Roulette durchführen können. Aber viele fragen sich, warum im Montageprozess bestimmte Probleme auftreten, wenn alle Messungen mehr als genau durchgeführt wurden.

Tatsache ist, dass der Schrank eingebaut isthorizontale Position und erst dann steigt und an die Wand montiert. Daher muss die Seitenwand des Schranks während des Anhebens der Struktur sowohl in der Höhe als auch diagonal des Raumes frei hindurchgehen.

Angenommen, es gibt einen Schrank mit einer Tiefe von 800 mm. Der Abstand vom Boden bis zur Decke beträgt 2600 mm. Ein erfahrener Möbelhersteller wird sagen, dass die Höhe des Schranks 126 mm weniger als die Höhe des Raumes betragen sollte. Aber warum auf 126 mm? Betrachten Sie das Beispiel.

Prüfen wir die Wirkung des Satzes des Pythagoras auf ideale Dimensionen des Kabinetts:

AC = √ AB²+ √BC²

AC = 2474²+800²= 2600 mm - alles konvergiert.

Angenommen, die Schrankhöhe beträgt nicht 2474 mm, sondern 2505 mm. Dann:

AC = 2505²+ 800²= 2629 mm.

Daher ist dieses Gehäuse nicht für die Installation in diesem Raum geeignet. Wie beim Anheben in eine vertikale Position können Sie den Körper beschädigen.

Vielleicht, verschiedene Beweismethoden in Betracht gezogenPythagoras Theorem von verschiedenen Wissenschaftlern können wir daraus schließen, dass es mehr als wahr ist. Jetzt können Sie die Informationen, die Sie in Ihrem täglichen Leben erhalten, nutzen und sich darauf verlassen, dass alle Berechnungen nicht nur nützlich, sondern auch wahr sind.