Schlussfolgerungen von Dirac. Dirac-Gleichung. Quantenfeldtheorie

Dieser Artikel ist dem Werk von Paul Dirac gewidmet,dessen Gleichung die Quantenmechanik stark bereichert hat. Es beschreibt die grundlegenden Konzepte, die notwendig sind, um die physikalische Bedeutung der Gleichung zu verstehen, sowie die Möglichkeiten, sie zu verwenden.

Wissenschaft und Wissenschaftler

Eine Person, die nicht mit Wissenschaft verbunden ist, repräsentiertder Prozess der Wissensgewinnung durch eine magische Aktion. Und Wissenschaftler sind nach Meinung solcher Leute Freaks, die eine unverständliche Sprache sprechen und leicht arrogant sind. Wenn er sich mit dem Forscher bekannt macht, sagt ein Mensch, der weit von der Wissenschaft entfernt ist, dass er die Physik in der Schule nicht verstanden hat. Auf diese Weise grenzt sich der Philister von wissenschaftlichen Erkenntnissen ab und bittet einen besser gebildeten Gesprächspartner, leichter und klarer zu sprechen. Sicher, Paul Dirac, dessen Gleichung wir in Erwägung ziehen, wurde auf die gleiche Weise begrüßt.

Elementarteilchen

Die Struktur der Materie wurde schon immer von Neugierigen gewecktGedanken. Im antiken Griechenland haben die Menschen bemerkt, dass die Marmorstufen, die viel Bein nahm, ändern Form im Laufe der Zeit, und schlug vor: jeder Fuß oder Sandale mit sich trägt ein winziges bisschen Materie. Diese Elemente wurden als "Atome" bezeichnet, das heißt "unteilbar". Name bleibt, aber es stellte sich heraus, dass die Atome und die Teilchen, die Atome bilden - die gleiche Verbindung, komplex. Diese Teilchen werden Elementarteilchen genannt. Es ist auf die Arbeit, die sie Dirac-Gleichung gewidmet, die nicht nur erlaubt, den Spin eines Elektrons zu erklären, aber auch darauf hin, die Anwesenheit von Antielektron.

Korpuskulärer Wellen-Dualismus

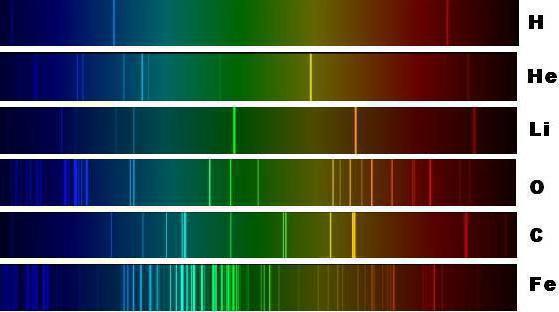
Die Entwicklung der Fotografie am EndeDas 19. Jahrhundert brachte nicht nur eine Mode für sich selbst, Nahrung und Katzen, sondern förderte auch die Möglichkeiten der Wissenschaft. Nachdem sie ein so bequemes Werkzeug wie ein schnelles Foto erhalten hatten (Erinnerung, bevor die Belichtung 30 bis 40 Minuten dauerte), begannen Wissenschaftler, eine Vielzahl von Spektren massiv aufzunehmen.

Die bestehenden Theorien der StrukturSubstanzen könnten die Spektren komplexer Moleküle nicht eindeutig erklären oder vorhersagen. Erstens hat die berühmte Erfahrung von Rutherford bewiesen, dass das Atom nicht so unteilbar ist: in seinem Zentrum befand sich ein schwerer positiver Kern, um den sich leicht negative Elektronen befanden. Die Entdeckung der Radioaktivität bewies dann, dass der Kern kein Monolith ist, sondern aus Protonen und Neutronen besteht. Die fast gleichzeitige Entdeckung des Energiequants, der Heisenbergschen Unschärferelation und der probabilistischen Lage der Elementarteilchen gaben der Entwicklung eines grundlegend anderen wissenschaftlichen Ansatzes für das Studium der Umwelt Auftrieb. Es gab einen neuen Abschnitt - die Physik der Elementarteilchen.

Das Hauptproblem zu Beginn dieses Jahrhunderts großer Entdeckungen im extrem kleinen Maßstab war die Erklärung der Anwesenheit von Elementarteilchen und der Masse und Eigenschaften der Welle.

Einstein bewies das sogar ein schwer fassbares PhotonEs hat Masse, als Feststoff einen Impuls überträgt, der auf dem (leicht Druck-Phänomen) fällt. In diesem Fall, wobei die zahlreichen Versuche zur Streuung von Elektronen in den Ritzen von mindestens sie die Beugung und Interferenz haben, ist es eigentümlich nur zu schwenken. Als Ergebnis musste ich zugeben: Elementarteilchen sind sowohl ein Objekt mit Masse als auch eine Welle. Das heißt, die Masse von beispielsweise dem Elektron wird zu einem Energiepaket mit Welleneigenschaften "verschmiert". Dieses Prinzip der Welle-Teilchen-Dualismus hat zunächst einmal zu erklären, warum erlaubt das Elektron in den Kern nicht fallen, und aus welchen Gründen gibt es in einem Atom Umlaufbahn, und die Übergänge zwischen ihnen sind abrupt. Diese Übergänge erzeugen ein Spektrum, das für jede Substanz einzigartig ist. Als nächstes Elementarteilchenphysik muss erklären war Eigenschaften der Teilchen selbst, sowie deren Wechselwirkungen.

Die Wellenfunktion und Quantenzahlen

Erwin Schrödinger hat eine erstaunliche und bis jetzt gemacht(eine unvollständige Entdeckung auf seiner Grundlage später, Paul Dirac baute seine Theorie auf). Er bewies, dass der Zustand eines Elementarteilchens, zum Beispiel eines Elektrons, durch die Wellenfunktion ψ beschrieben wird. Es bedeutet nichts für sich, aber sein Quadrat wird die Wahrscheinlichkeit zeigen, ein Elektron an einer bestimmten Stelle im Raum zu finden. Der Zustand eines Elementarteilchens in einem Atom (oder einem anderen System) wird durch vier Quantenzahlen beschrieben. Dies ist die Haupt (n), Orbital (l), magnetische (m) und Spin (m_s) der Nummer. Sie zeigen die Eigenschaften eines Elementarteilchens. Als eine Analogie können Sie eine Stange Öl bringen. Seine Eigenschaften - Gewicht, Größe, Farbe und Fett. Die Eigenschaften, die Elementarteilchen beschreiben, können jedoch nicht intuitiv verstanden werden, sie müssen durch eine mathematische Beschreibung realisiert werden. Diracs Arbeit, deren Gleichung im Mittelpunkt dieses Artikels steht, ist der letzten Spinzahl gewidmet.

Drehen

Bevor man direkt zu der Gleichung übergeht, ist es notwendig zu erklären, was die Spinzahl m ist_s. Es zeigt das intrinsische Moment des Impulses eines Elektrons und anderer Elementarteilchen. Diese Zahl ist immer positiv und kann einen ganzzahligen Wert annehmen, null oder halbzahlig (für ein Elektron m_s = 1/2). Spin ist ein Vektorwert und der einzige, der die Orientierung eines Elektrons beschreibt. Die Quantenfeldtheorie stellt den Spin auf die Grundlage der Austauschwechselwirkung, zu der es in der normalerweise intuitiven Mechanik kein Analoges gibt. Die Spin-Nummer zeigt an, wie sich der Vektor drehen soll, um in den ursprünglichen Zustand zu kommen. Ein Beispiel ist ein gewöhnlicher Kugelschreiber (der Schreibteil ist eine positive Richtung des Vektors). Um es in den ursprünglichen Zustand zu bringen, muss es um 360 Grad gedreht werden. Diese Situation entspricht einem Spin gleich 1. Für einen Spin 1/2, wie ein Elektron, sollte die Rotation 720 Grad betragen. Neben mathematischen Instinkten muss man daher ein räumliches Denken entwickelt haben, um diese Eigenschaft zu verstehen. Ein wenig darüber sprachen wir über die Wellenfunktion. Es ist der Hauptakteur der Schrödinger-Gleichung, die den Zustand und die Position eines Elementarteilchens beschreibt. Aber diese Beziehung in ihrer ursprünglichen Form ist für Teilchen ohne Spin gedacht. Wir können den Zustand des Elektrons nur beschreiben, wenn wir die Schrödinger-Gleichung verallgemeinern, die in Diracs Arbeit gemacht wurde.

Bosonen und Fermionen

Fermion ist ein Teilchen mit einem halbzahligen Spinwert. Fermionen sind in Systemen (zum Beispiel Atomen) nach dem Pauli-Prinzip angeordnet: In jedem Zustand sollte es nicht mehr als ein Teilchen geben. In einem Atom unterscheidet sich jedes Elektron irgendwie von allen anderen (einige Quantenzahlen haben eine andere Bedeutung). Die Quantenfeldtheorie beschreibt auch einen anderen Fall - Bosonen. Sie haben eine ganze Drehung und können alle in einem Zustand gleichzeitig sein. Die Implementierung dieses Falles wird Bose-Kondensation genannt. Trotz der bewährten theoretischen Möglichkeit, es zu bekommen, wurde es praktisch erst 1995 realisiert.

Dirac-Gleichung

Wie wir oben sagten, brachte Paul DiracGleichung des klassischen Elektronenfeldes. Es beschreibt auch die Zustände anderer Fermionen. Die physikalische Bedeutung der Beziehung ist komplex und vielschichtig, und aus ihrer Form ergeben sich viele grundsätzliche Schlussfolgerungen. Die Art der Gleichung ist wie folgt:

- (mc² α₀+ c Σ a_kp_k {k = 0-3}) ψ (x, t) = i ħ {∂ ∂ / ∂ t (x, t)},

wo m Ist die Masse des Fermion (insbesondere das Elektron), mit dem - Lichtgeschwindigkeit, p_k- drei Impulskomponenten-Operatoren (entlang der x-, y-, z-Achsen), ħ - die reduzierte Planck-Konstante, x und t - drei räumliche Koordinaten (entsprechen den X-, Y-, Z-Achsen) bzw. Zeit und ψ(x, t) - Vier-Komponenten-komplexe Wellenfunktion, α_k (k = 0, 1, 2, 3) sind Pauli-Matrizen. Letztere sind lineare Operatoren, die auf die Wellenfunktion und ihren Raum einwirken. Diese Formel ist ziemlich kompliziert. Um zumindest seine Komponenten zu verstehen, ist es notwendig, die grundlegenden Definitionen der Quantenmechanik zu verstehen. Sie sollten auch über bemerkenswerte mathematische Kenntnisse verfügen, um zumindest zu wissen, was ein Vektor, eine Matrix und ein Operator sind. Eine fachmännische Sicht auf die Gleichung wird noch mehr sagen als ihre Komponenten. Eine Person, die mit der Kernphysik vertraut ist und mit der Quantenmechanik vertraut ist, wird die Bedeutung dieser Beziehung verstehen. Es muss jedoch zugegeben werden, dass die Dirac- und Schrödinger-Gleichungen nur die elementaren Grundlagen der mathematischen Beschreibung von Prozessen sind, die in der Welt der Quantengrößen auftreten. Theoretische Physiker, die sich entschieden haben, sich den Elementarteilchen und ihrer Wechselwirkung zu widmen, sollten das Wesen dieser Beziehungen im ersten und zweiten Kurs des Instituts verstehen. Aber diese Wissenschaft ist faszinierend, und auf diesem Gebiet können Sie einen Durchbruch erzielen oder Ihren Namen verewigen, indem Sie ihn einer Gleichung, Transformation oder Eigenschaft zuordnen.

Physische Bedeutung der Gleichung

Wie wir versprochen haben, erzählen wir, welche Schlüsse daraus hervorgehenDirac-Gleichung für Elektron. Zunächst wird aus dieser Beziehung klar, dass der Elektronenspin gleich 1/2 ist. Zweitens hat das Elektron gemäß der Gleichung sein eigenes magnetisches Moment. Es ist gleich dem Bohr-Magneton (Einheit des elementaren magnetischen Moments). Das wichtigste Ergebnis dieser Beziehung liegt jedoch im nicht wahrnehmbaren Operator α_k. Ableitung der Dirac-Gleichung aus der Schrödinger-Gleichunghat lange gedauert. Zuerst dachte Dirac, dass diese Operatoren die Beziehung störten. Mit Hilfe verschiedener mathematischer Tricks versuchte er sie von der Gleichung auszuschließen, scheiterte jedoch. Als Ergebnis enthält die Dirac-Gleichung für ein freies Teilchen vier Operatoren α. Jeder von ihnen ist eine Matrix [4x4]. Zwei entsprechen der positiven Masse eines Elektrons, die die Anwesenheit von zwei Positionen seines Spins beweist. Die anderen beiden geben eine Lösung für die negative Partikelmasse. Die einfachste Kenntnis der Physik gibt einer Person die Möglichkeit zu schließen, dass dies in der Realität unmöglich ist. Aber als Ergebnis des Experiments stellte sich heraus, dass die letzten beiden Matrizen Lösungen für ein existierendes Teilchen sind, das einem Elektron entgegengesetzt ist - ein Antielektron. Wie ein Elektron hat ein Positron (so genanntes Teilchen) eine Masse, aber seine Ladung ist positiv.

Positron

Wie so oft in der Ära der Quantenentdeckungen, DiracZuerst glaubte ich meiner Schlussfolgerung nicht. Er wagte nicht, die Vorhersage eines neuen Teilchens offen zu veröffentlichen. Zwar hat der Wissenschaftler in vielen Artikeln und auf verschiedenen Symposien die Möglichkeit seiner Existenz betont, obwohl er dies nicht postulierte. Aber bald nach dem Abschluss dieses berühmten Verhältnisses wurde das Positron in der Zusammensetzung der kosmischen Strahlung gefunden. Somit wurde seine Existenz empirisch bestätigt. Positron ist das erste Element der von Menschen gefundenen Antimaterie. Ein Positron wird als eines der Zwillinge eines Paares (der andere Zwilling ist ein Elektron) geboren, wenn hochenergetische Photonen mit Materiekernen in einem starken elektrischen Feld interagieren. Wir geben keine Zahlen (der interessierte Leser selbst findet alle notwendigen Informationen). Es sollte jedoch betont werden, dass dies eine kosmische Skala ist. Nur Supernova-Explosionen und Kollisionen von Galaxien können Photonen der benötigten Energie erzeugen. Sie sind auch in einer gewissen Menge in den Kernen heißer Sterne, einschließlich der Sonne, enthalten. Aber der Mensch sucht immer seinen eigenen Nutzen. Die Vernichtung von Materie mit Antimaterie gibt viel Energie. Um diesen Prozess einzudämmen und zum Wohle der Menschheit zu starten (zum Beispiel würden interstellare Flugzeugtriebwerke für die Vernichtung wirksam sein), lernten die Menschen, wie man unter Laborbedingungen Protonen herstellt.

Insbesondere große Beschleuniger (wie Hadroncollider) kann Elektron-Positron-Paare erzeugen. Zuvor wurde auch vorgeschlagen, dass es nicht nur elementare Antiteilchen (neben einem Elektron gibt es mehrere mehr), sondern auch ganze Antimaterie gibt. Selbst ein sehr kleines Stück eines Antimaterie-Kristalls würde Energie für den gesamten Planeten liefern (vielleicht war Superman Kryptonit Antimaterie?).

Aber leider ist die Erzeugung von Antimaterie schwerer als Kerne.Wasserstoff im vorhersehbaren Universum wurde nicht dokumentiert. Wenn der Leser jedoch denkt, dass die Wechselwirkung einer Substanz (wir betonen, dass es sich um eine Substanz und nicht ein einzelnes Elektron handelt) mit einem Positron sofort in der Vernichtung endet, dann irrt er sich. Beim Abbremsen eines Positrons mit hoher Geschwindigkeit in einigen Flüssigkeiten mit einer von Null verschiedenen Wahrscheinlichkeit entsteht ein gebundenes Elektron-Positron-Paar, das Positronium genannt wird. Diese Formation hat einige Eigenschaften des Atoms und ist sogar in der Lage, chemische Reaktionen einzugehen. Aber dieses zerbrechliche Tandem existiert für eine kurze Zeit und vernichtet dann sowieso mit der Emission von zwei und in einigen Fällen von drei Gammaquanten.

Nachteile der Gleichung

Obwohl aufgrund dieses VerhältnissesAntielektron und Antimaterie wurden nachgewiesen, es hat einen erheblichen Nachteil. Das Schreiben einer Gleichung und eines darauf basierenden Modells kann nicht vorhersagen, wie Partikel entstehen und zerstört werden. Das ist eine eigentümliche Ironie der Quantenwelt: Eine Theorie, die die Geburt von Materie-Antimaterie-Paaren vorhergesagt hat, kann diesen Prozess nicht adäquat beschreiben. Dieser Mangel wurde in der Quantenfeldtheorie eliminiert. Durch die Einführung der Quantisierung von Feldern beschreibt dieses Modell ihre Wechselwirkung, einschließlich der Entstehung und Zerstörung von Elementarteilchen. Mit "Quantenfeldtheorie" ist in diesem Fall ein sehr spezifischer Begriff gemeint. Dies ist ein Gebiet der Physik, das das Verhalten von Quantenfeldern untersucht.

Dirac-Gleichung in zylindrischen Koordinaten

Um zu beginnen, lassen Sie uns sagen, dass ein solcher zylindrischerKoordinatensystem. Anstelle der üblichen drei zueinander senkrechten Achsen werden Winkel, Radius und Höhe verwendet, um die genaue Position eines Punktes im Raum zu bestimmen. Dies ist das gleiche wie das Polarkoordinatensystem in der Ebene, nur die dritte Dimension, die Höhe, wird hinzugefügt. Dieses System ist praktisch, wenn Sie eine bestimmte Oberfläche beschreiben oder erkunden möchten, die symmetrisch zu einer der Achsen ist. Für die Quantenmechanik ist dies ein sehr nützliches und praktisches Werkzeug, mit dem Sie die Größe von Formeln und die Anzahl der Berechnungen erheblich reduzieren können. Dies ist eine Folge der Achsensymmetrie der Elektronenwolke im Atom. Die Dirac-Gleichung in Zylinderkoordinaten wird etwas anders gelöst als im üblichen System und liefert manchmal unerwartete Ergebnisse. Zum Beispiel wurden einige angewandte Probleme der Bestimmung des Verhaltens von Elementarteilchen (meistens Elektronen) in einem quantisierten Feld gelöst, indem die Form der Gleichung in zylindrische Koordinaten umgewandelt wurde.

Verwenden Sie die Gleichung, um die Struktur von Partikeln zu bestimmen

Diese Gleichheit beschreibt einfache Teilchen: diejenigen, die nicht aus noch kleineren Elementen bestehen. Die moderne Wissenschaft ist in der Lage, magnetische Momente mit einer ausreichend hohen Genauigkeit zu messen. Somit wird die Diskrepanz des experimentell gemessenen Werts mit dem magnetischen Moment, das unter Verwendung der Dirac-Gleichung berechnet wird, indirekt die komplexe Struktur des Teilchens anzeigen. Daran erinnern, dass diese Gleichheit für Fermionen gilt, ihr Spin ist halbzahlig. Mit dieser Gleichung wurde die komplexe Struktur von Protonen und Neutronen bestätigt. Jeder von ihnen besteht aus noch kleineren Elementen, die Quarks genannt werden. Das Gluonfeld hält Quarks zusammen und verhindert, dass sie auseinander fallen. Es gibt eine Theorie, dass Quarks nicht die elementarsten Teilchen unserer Welt sind. Aber während die Leute nicht genug technische Macht haben, um es zu überprüfen.