Regression in Excel: Gleichung, Beispiele. Lineare Regression

Die Regressionsanalyse ist eine statistische MethodeEine Studie, die die Abhängigkeit eines Parameters von einer oder mehreren unabhängigen Variablen zeigt. In der Vorcomputer-Ära war seine Verwendung ziemlich schwierig, insbesondere wenn es sich um große Datenmengen handelte. Heute, nachdem Sie gelernt haben, eine Regression in Excel zu erstellen, können Sie komplexe statistische Probleme in nur wenigen Minuten lösen. Im Folgenden finden Sie spezifische Beispiele aus dem Bereich der Wirtschaftswissenschaften.

Arten der Regression

Das Konzept wurde 1886 von Francis Galton in die Mathematik eingeführt. Regression passiert:

linear;
parabolisch;
Machtgesetz;
exponentiell;
hyperbolisch;
Indikativ;
logarithmisch.

Beispiel 1

Betrachten wir das Problem der Bestimmung der Abhängigkeit der Anzahl der pensionierten Mitglieder des Kollektivs vom Durchschnittsgehalt von 6 Industrieunternehmen.

Die Aufgabe. Sechs Unternehmen haben das durchschnittliche Monatsgehalt und die Anzahl der Mitarbeiter analysiert, die freiwillig verlassen. In tabellarischer Form haben wir:

	A	B	C
1	X	Anzahl der Resignierten	Gehalt
2	X	y	30000 Rubel
3	1	60	35.000 Rubel
4	2	35	40000 Rubel
5	3	20	45.000 Rubel
6	4	20	50.000 Rubel
7	5	15	55.000 Rubel
8	6	15	60000 Rubel

Für das Problem der Bestimmung der Abhängigkeit der Anzahl von Mitarbeitern, die bei 6 Unternehmen dem Durchschnittsgehalt überlassen wurden, hat das Regressionsmodell die Form der Gleichung Y = a₀ + a₁x₁ + ... + a_kx_k, wo x_ich - Einflussgrößen, a_ich - Koeffizienten der Regression und k - Anzahl der Faktoren.

Für diese Aufgabe ist Y der Indikator für die ausgeschiedenen Mitarbeiter und der Einflussfaktor ist das Gehalt, das mit X bezeichnet wird.

Verwenden des Excel-Tabellenprozessors

Der Analyse der Regression in Excel muss vorausgegangen seinAnwendung von integrierten Funktionen auf die verfügbaren Daten. Für diese Zwecke ist es jedoch besser, das sehr nützliche Add-on "Analysepaket" zu verwenden. Um es zu aktivieren, benötigen Sie:

Von der Registerkarte "Datei" gehen Sie zum Abschnitt "Optionen";
Im geöffneten Fenster wählen Sie die Zeile "Add-Ins";
Klicken Sie auf den "Go" -Button, der sich unterhalb der "Management" -Linie befindet;
Setzen Sie ein Häkchen neben dem Namen "Analysepaket" und bestätigen Sie Ihre Aktionen mit "Ok".

Wenn dies richtig ausgeführt wird, wird die rechte Schaltfläche auf der rechten Seite der Registerkarte Daten über dem Excel-Arbeitsblatt angezeigt.

Lineare Regression in Excel

Jetzt, da wir alle notwendigen virtuellen Instrumente zur Verfügung haben, um ökonometrische Berechnungen durchzuführen, können wir damit beginnen, unser Problem zu lösen. Dafür:

Klicken Sie auf den Button "Datenanalyse";
Im geöffneten Fenster klicken Sie auf den Button "Regression";
In der erscheinenden Registerkarte geben wir den Wertebereich für Y (die Anzahl der Mitarbeiter, die gegangen sind) und für X (ihr Gehalt) ein;
Wir bestätigen unsere Aktionen, indem wir auf "OK" klicken.

Als Ergebnis wird das Programm automatisch ausgefülltneue tabellarische Tabellenprozessor-Datenregressionsanalyse. Beachten Sie! In Excel besteht die Möglichkeit, den von Ihnen bevorzugten Ort selbst festzulegen. Dies könnte beispielsweise das gleiche Blatt wie die Y- und X-Werte oder sogar ein neues Buch sein, das speziell zum Speichern solcher Daten entwickelt wurde.

Analyse der Regressionsergebnisse für das R-Quadrat

In Excel haben die Daten, die während der Verarbeitung der Daten des betreffenden Beispiels erhalten werden, die Form:

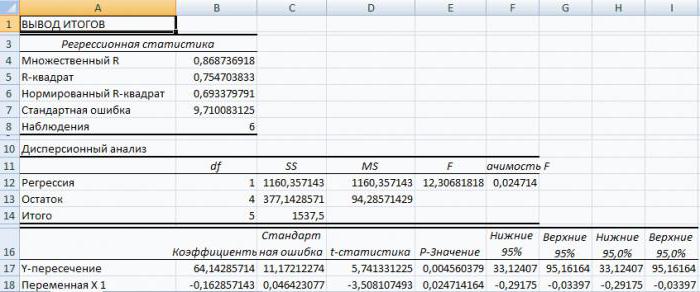
Vor allem ist es notwendig, darauf zu achtender Wert des R-Quadrats. Es ist das Bestimmtheitsmaß. In diesem Beispiel ist das R-Quadrat = 0,755 (75,5%), dh die berechneten Parameter des Modells erklären die Abhängigkeit zwischen den betrachteten Parametern mit 75,5%. Je höher der Wert des Bestimmtheitsmaßes ist, desto ausgewogener wird das gewählte Modell für eine bestimmte Aufgabe. Es wird angenommen, dass es die reale Situation mit einem R-Quadrat-Wert über 0,8 korrekt beschreibt. Wenn das R-Quadrat <0,5 ist, kann eine solche Analyse der Regression in Excel nicht als sinnvoll angesehen werden.

Die Analyse der Koeffizienten

Die Zahl 64.1428 zeigt, wie hoch der Wert von Y sein wird.wenn alle Variablen xi im betrachteten Modell zurückgesetzt werden. Mit anderen Worten, es kann argumentiert werden, dass der Wert des analysierten Parameters durch andere Faktoren beeinflusst wird, die in einem bestimmten Modell nicht beschrieben sind.

Der folgende Koeffizient ist -0.166285, gelegen inZelle B18, zeigt den Wichtungseffekt der Variablen X auf Y. Das bedeutet, dass das durchschnittliche Monatsgehalt der Beschäftigten innerhalb des betrachteten Modells die Anzahl derjenigen betrifft, die mit einem Gewicht von -0,16285 weggegangen sind, das heißt, der Grad ihres Einflusses ist sehr gering. Das Zeichen "-" zeigt an, dass der Koeffizient einen negativen Wert hat. Dies ist offensichtlich, da jeder weiß, dass je höher das Gehalt im Unternehmen ist, desto weniger Menschen den Wunsch äußern, den Arbeitsvertrag zu kündigen oder zu verlassen.

Mehrfache Regression

Mit diesem Begriff meinen wir die Gleichung der Verbindung mit mehreren unabhängigen Variablen der Form:

y = f (x₁+ x₂+ ... x_m) + ε, wobei y das resultierende Attribut (abhängige Variable) und x ist₁, x₂, ... x_m- Dies sind Vorzeichen (unabhängige Variablen).

Auswertung der Parameter

Für die multiple Regression (MP) wird sie mit der Methode der kleinsten Quadrate (OLS) durchgeführt. Für lineare Gleichungen der Form Y = a + b₁x₁ + ... + b_mx_m+ ε Wir konstruieren ein System von Normalgleichungen (siehe unten)

Um den Grundsatz der Methode zu verstehen, betrachten Sie den Zwei-Faktoren-Fall. Dann haben wir eine Situation, die durch Formel beschrieben wird

Daher erhalten wir:

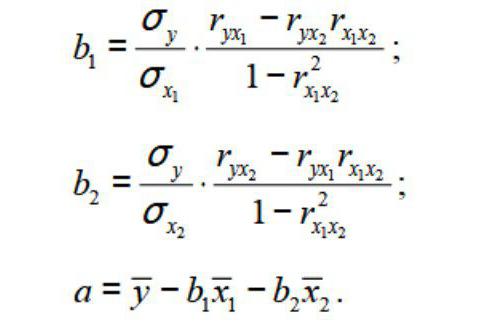
wobei σ die Varianz des entsprechenden Merkmals ist, das sich im Index widerspiegelt.

Der OLS ist auf die MP-Gleichung in einem standardisierten Maßstab anwendbar. In diesem Fall erhalten wir die Gleichung:

in welcher t_y, t_x_{1, ...}t_xm-standardisierte Variablen, für die die Durchschnittswerte 0 sind; β_ich - standardisierte Regressionskoeffizienten und die Standardabweichung ist 1.

Beachten Sie, dass alle β_ichIn diesem Fall werden sie als normalisiert und angegebenzentralisiert, so dass ihr Vergleich untereinander als richtig und zulässig angesehen wird. Außerdem ist es üblich, Faktoren auszusortieren und diejenigen zu verwerfen, die die niedrigsten Werte von βi aufweisen.

Das Problem mit der linearen Regressionsgleichung

Angenommen, es gibt eine Tabelle der Preisdynamik einer bestimmten Ware N innerhalb der letzten 8 Monate. Es ist notwendig, eine Entscheidung über die Zweckmäßigkeit des Kaufs seiner Charge zu einem Preis von 1.850 Rubel pro Tonne zu treffen.

	A	B	C
1	Monatsnummer	Name des Monats	Rohstoffpreis N
2	1	Januar	1750 Rubel pro Tonne
3	2	Februar	1755 Rubel pro Tonne
4	3	März	1767 Rubel pro Tonne
5	4	April	1760 Rubel pro Tonne
6	5	Mai	1770 Rubel pro Tonne
7	6	Juni	1790 Rubel pro Tonne
8	7	Juli	1810 Rubel pro Tonne
9	8	August	1840 Rubel pro Tonne

Um dieses Problem in einem Tabellenprozessor zu lösen„Excel“ benötigt aus den obigen Beispielen bereits bekannt zu verwenden, die „Data Analysis“ -Tool. Als nächstes wählen Sie „Regression“ Abschnitt und Parameter. Es ist zu beachten, dass im Feld "Eingabeintervall Y" der Wertebereich für die abhängige Variable (in diesem Fall die Preise für die Waren in bestimmten Monaten des Jahres) und im "Erfassungsintervall X" für das Independent (Monatsnummer) eingegeben werden soll. Wir bestätigen die Aktion «OK» klicken. In einem neuen Arbeitsblatt (falls angegeben), so erhalten wir die Daten für die Regression.

Wir bauen auf ihnen eine lineare Gleichung der Form y = ax + b, wobeidie Parameter a und b sind die Koeffizienten der Zeile mit dem Namen der Monatsnummer und der Koeffizienten und die Zeilen "Y-Schnitt" aus dem Blatt mit den Ergebnissen der Regressionsanalyse. Daher wird die lineare Regressionsgleichung (VR) für Problem 3 geschrieben als:

Der Preis der Ware N = 11.714 * die Zahl des Monats + 1727,54.

oder in algebraischer Notation

y = 11,714 x + 1727,54

Analyse der Ergebnisse

Um zu entscheiden, ob die resultierende Gleichunglineare Regression, die Koeffizienten der multiplen Korrelation (KMC) und Bestimmung, sowie das Fisher-Kriterium und der Student-Test werden verwendet. In der Excel-Tabelle mit Regressionsergebnissen erscheinen sie unter den Namen von mehreren R-, R-Quadrat-, F-Statistiken bzw. T-Statistiken.

KMK R ermöglicht die Schätzung der DichtheitProbabilistische Beziehung zwischen unabhängigen und abhängigen Variablen. Sein hoher Wert weist auf eine ziemlich starke Beziehung zwischen den Variablen "Nummer des Monats" und "Preis der Güter N in Rubel pro 1 Tonne" hin. Die Art dieser Beziehung bleibt jedoch unbekannt.

Das Quadrat des Bestimmtheitsmaßes R²(RI) ist eine numerische EigenschaftAnteil der Gesamtspreizung und zeigt die Streuung von welchem Teil der experimentellen Daten, d.h. Die Werte der abhängigen Variablen entsprechen der linearen Regressionsgleichung. In dem betrachteten Problem beträgt dieser Wert 84,8%, dh die statistischen Daten werden mit hoher Genauigkeit durch die empfangene SD beschrieben.

F-Statistik, auch Fisher-Kriterium genannt, wird verwendet, um die Signifikanz linearer Abhängigkeit zu bewerten, indem die Hypothese ihrer Existenz widerlegt oder bestätigt wird.

Der Wert von t-statistics (Student's test) hilft, die Bedeutung des Koeffizienten für einen unbekannten oder freien Ausdruck der linearen Abhängigkeit zu bewerten. Wenn der Wert des t-Tests> t_crdann wird die Hypothese der Geringfügigkeit des freien Terms der linearen Gleichung zurückgewiesen.

In der Problematik für die freie LaufzeitMit den Excel-Tools wurde festgestellt, dass t = 169.20903 und p = 2.89E-12, das heißt, wir haben die Null-Wahrscheinlichkeit, dass die korrekte Hypothese über die Bedeutungslosigkeit des freien Terms zurückgewiesen wird. Für den Koeffizienten mit unbekanntem t = 5.79405 und p = 0.001158. Mit anderen Worten, die Wahrscheinlichkeit, dass die korrekte Hypothese über die Geringfügigkeit des Koeffizienten für das Unbekannte zurückgewiesen wird, beträgt 0,12%.

Somit kann argumentiert werden, dass die resultierende lineare Regressionsgleichung angemessen ist.

Das Problem der Zweckmäßigkeit des Kaufs eines Aktienpakets

Die Mehrfachregression in Excel wird mit demselben Tool "Datenanalyse" durchgeführt. Lassen Sie uns ein spezifisches angewandtes Problem betrachten.

Die Verwaltungsgesellschaft "NNN" sollte eine Entscheidung treffenauf die Zweckmäßigkeit des Kaufs einer 20% -Beteiligung an MMM. Die Kosten für das Paket (SP) betragen 70 Millionen US-Dollar. Spezialisten von "NNN" haben Daten über ähnliche Transaktionen gesammelt. Es wurde beschlossen, den Wert der Beteiligung an solchen Parametern, ausgedrückt in Millionen US-Dollar, wie folgt zu bewerten:

Kreditoren (VK);
Jahresumsatz (VO);
Debitorenbuchhaltung (VD);
Wert des Anlagevermögens (SOF).

Darüber hinaus wird der Parameter verwendet Enterprise Gehaltsrückstände (V3 P) in Tausenden von US-Dollar.

Lösung mittels Excel-Tabellenkalkulationsprozessor

Zunächst ist es notwendig, eine Tabelle mit Quelldaten zu erstellen. Es hat die folgende Form:

Weiter:

Rufen Sie das Fenster "Datenanalyse" auf;
Wählen Sie den Abschnitt "Regression";
Geben Sie im Fenster "Eingabeintervall Y" den Wertebereich der abhängigen Variablen aus Spalte G ein;
Klicken Sie auf das Symbol mit dem roten Pfeil rechts neben dem Fenster "Eingabeintervall X" und wählen Sie auf dem Blatt den Bereich aller Werte aus den Spalten B, C, D, F.

Markieren Sie den Punkt "Neues Arbeitsblatt" und klicken Sie auf "OK".

Holen Sie sich die Regressionsanalyse für diese Aufgabe.

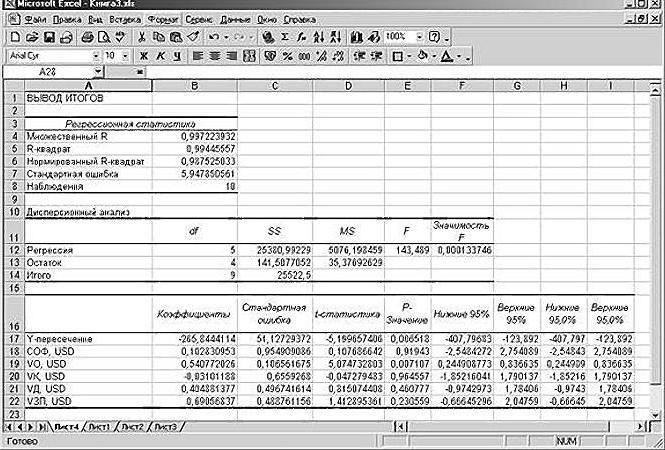
Untersuchung der Ergebnisse und Schlussfolgerungen

"Wir sammeln" aus den gerundeten Daten, die oben auf einem Blatt eines Excel-Tabellenkalkulationsprozessors dargestellt sind, die Regressionsgleichung:

SP = 0,103 · SOF + 0,541 · VO - 0,031 · VK + 0,405 · VD + 0,691 · VZP - 265,844.

In einer vertrauteren mathematischen Form kann es geschrieben werden als:

y = 0,103 · x1 + 0,541 · x2 - 0,031 · x3 + 0,405 · x4 + 0,691 · x5 - 265,844

Die Daten für MMM sind in der Tabelle dargestellt:

SOF, USD	VO, USD	VK, USD	VD, USD	VZP, USD	SP, USD
102,5	535,5	45,2	41,5	21,55	64,72

Ersetzen sie in die Regressionsgleichung, erhaltendie Zahl beträgt 64,72 Millionen US-Dollar. Dies bedeutet, dass die Aktien von JSC MMM nicht erworben werden sollten, da ihr Wert von 70 Millionen US-Dollar ziemlich hoch ist.

Wie Sie sehen können, ermöglichte die Verwendung des Excel-Tabellenprozessors und der Regressionsgleichung eine fundierte Entscheidung über die Durchführbarkeit einer sehr spezifischen Transaktion.

Jetzt wissen Sie, was Regression ist. Die oben diskutierten Beispiele in Excel werden Ihnen bei der Lösung praktischer Probleme auf dem Gebiet der Ökonometrie helfen.